The axis of symmetry is a hypothetical straight line that splits a form into two identical pieces, resulting in one portion being the mirror image of the other. When the two pieces are folded along the axis of symmetry, they superimpose. The straight line is also known as the line of symmetry/mirror line. This line might be horizontal, vertical, or slanted. This axis of symmetry may be seen in nature, such as flowers, riverbanks, structures, leaves, and so forth. The Taj Mahal, India’s most famous marble monument, has an axis of symmetry.
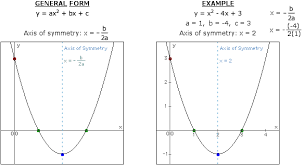
The axis of symmetry is a concept utilized in graphing algebraic formulas that result in parabolas or roughly u-shaped shapes. These are known as quadratic functions, and their equation typically looks like this: y = ax2 + bx + c. The variable a cannot have a value of zero. The simplest of these functions is y = x2, where the vertex or precise middle line going along the parabola, also known as the axis of symmetry, is the graph’s y-axis or x = 0. It cuts the parabola in half straight, and everything on either side of it progresses symmetrically.
What Is The Axis Of Symmetry?
The term “symmetry” connotes balance. Symmetry can be used in a variety of contexts and situations. A marriage, for example, maybe considered to have symmetry if each partner has equal participation in financial decision-making. However, because such issues are not always clear-cut, we shall limit our discussion today to mathematical settings.
In geometry, symmetry is discovered when a figure can be split into two halves that are precise mirrors of each other, as seen in Figure below Line symmetry is seen in these figures. If we folded each figure in half along the red lines of symmetry, the two halves would be perfectly symmetrical.
An axis of symmetry is an imaginary line drawn across a form that creates a mirror image on each side.
Axis of symmetry definition: A straight line that connects every point on a given curve with another point so that the line connecting the two locations is bisected by the provided line
Axis Of Symmetry Equation
A parabola is the graph of a quadratic function. A parabola’s axis of symmetry is a vertical line that splits the parabola into two congruent halves. The axis of symmetry always goes through the parabola’s vertex. The x-coordinate of the vertex is the equation of the parabola’s axis of symmetry.
Let’s look at the axis of the symmetry equation:
Equation Of Axis Of Symmetry:
The axis of symmetry for a quadratic function in standard form, y=ax2+bx+c, is a vertical line x= -b2a.
Let’s take an example to understand the equation for the axis of symmetry:
Example 1:
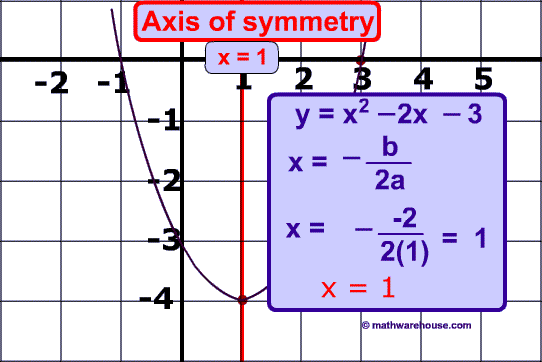
Find the axis of symmetry of the graph of y = $x^{2}$−6x+5, using the formula.
Solution:
Given,
y = x2 – 6x + 5
For a quadratic function in standard form, y = a$x^{2}$+bx+c, the axis of symmetry is a vertical line, x = $\frac{-b}{2a}$
Here, a = 1, b = −6 and c = 5
Substituting the values of a and b,
x = -(-6)/2(1)
= 6/2
= 3
Therefore, the axis of symmetry is x = 3.
Read Here– Best Way To Learn Spanish Fluently
How To Find The Axis Of Symmetry: Axis Of Symmetry Formula
The axis of symmetry is a fictitious straight line that splits an object into two identical pieces or makes it symmetrical.
The axis of symmetry formula is used to calculate the axis of symmetry of a parabola when applied to quadratic equations with the standard form of the equation and the line of symmetry. The axis of symmetry is a line that splits or bifurcates any object into two equal halves, both of which are mirror copies of each other. This axis line dividing the items might be of any of three types: horizontal (x-axis), vertical (y-axis), or inclined axis. A line of symmetry in geometry denotes a line that divides a geometric form into two equal halves, resulting in a mirror image.
The axis of the symmetry equation can be written in two ways:
Formalized form
- Vertex shape
- Formalized form
In standard form, the quadratic equation is y = ax2+ b x+c.
where a and b are “x” coefficients and c is the constant form
The axis of symmetry formula, in this case, is: x = – b/2a
In vertex form, the quadratic equation is y=a (x-h)2 + k.
where (h, k) is the parabola’s vertex Because the axis of symmetry and the vertex are on the same line, we can state x = h in vertex form: h = -b/2a
Let’s see how to find the axis of symmetry by taking an example:
Take this quadratic equation for example 2x2 + 3x -1
Step 1: Determine the degree of your polynomial. A polynomial’s degree (or “order”) is simply the greatest exponent value in the equation. If the degree of your polynomial is 2 i.e you have no exponent greater than x2, you may use this approach to identify the axis of symmetry. Method 2 should be used if the degree of the polynomial is more than 2.
As an example, consider the polynomial 2x2 + 3x – 1. The greatest exponent present is x2, indicating that it is a 2nd order polynomial, and you may use this first technique to determine the axis of symmetry.
Step 2: Input your data into the axis of the symmetry formula. Use the fundamental formula x = -b / 2a to find the axis of symmetry for a 2nd order polynomial of the type ax2 + bx +c (a parabola).
In the above example, a = 2, b = 3, and c = -1. If you plug these numbers into your calculation, you’ll get: x = -3 / 2(2) = -3/4.
Let’s solve a question
Example: If the axis of symmetry of the equation y = qx2 – 32x – 10 is 8, then find the value of q
Solution: Given,
y = qx2 – 32x – 10
Axis of symmetry = x = 8
Applying the axis of symmetry formula in the standard form of the quadratic equation:
x = -b/2a
where a = q, b = -32 and x = 8
8 = -(-32)/2 × q
8 = 32/2q
16q = 32
q = 2
Therefore, the value of q = 2
Axis Of Symmetry Calculator
How does an axis of symmetry calculator work?The following procedures are used by an online calculator to determine the exact position of the axis of symmetry:
Input: To find the axis of symmetry, enter an equation.
Calculate by pressing the button.
Output: The axis of the symmetry equation calculator generates an axis of symmetry equation for the supplied problem and provides a step-by-step solution.
How To Find Axis Of Symmetry Of A Parabola?
More complicated quadratic functions are frequently required to be graphed, and the axis of symmetry will not be as readily split by the y-axis. Instead, depending on the equation, it will be to the left or right of it and may require some function manipulation to find out. It is critical to determine the vertex or beginning point of the parabola since its x-coordinate is equivalent to the axis of symmetry. It greatly simplifies charting the remainder of the parabola.
Let’s look at the axis of symmetry parabola formula
4𝑝(𝑦−𝑘)=(𝑥−ℎ)2
V=(h,k) is the vertex of the parabola and
p is the distance from the vertex to the focus (and also from the vertex to the directrix). If
- p>0, the parabola opens upward
- p<0, the parabola opens downward
Go! Solve Problems Of Axis Of Symmetry
As the saying goes, practice makes a man perfect. Go and try out some problems.
Though this type of graphing and determining the axis of symmetry might take some time theoretically, it is a valuable idea in mathematics and algebra. It is usually taught after students have spent some time working with quadratic equations and knowing how to do some fundamental operations on them, such as factoring. This topic is introduced to most students in the late first year of algebra, and it may be revisited in more sophisticated forms in subsequent math studies.