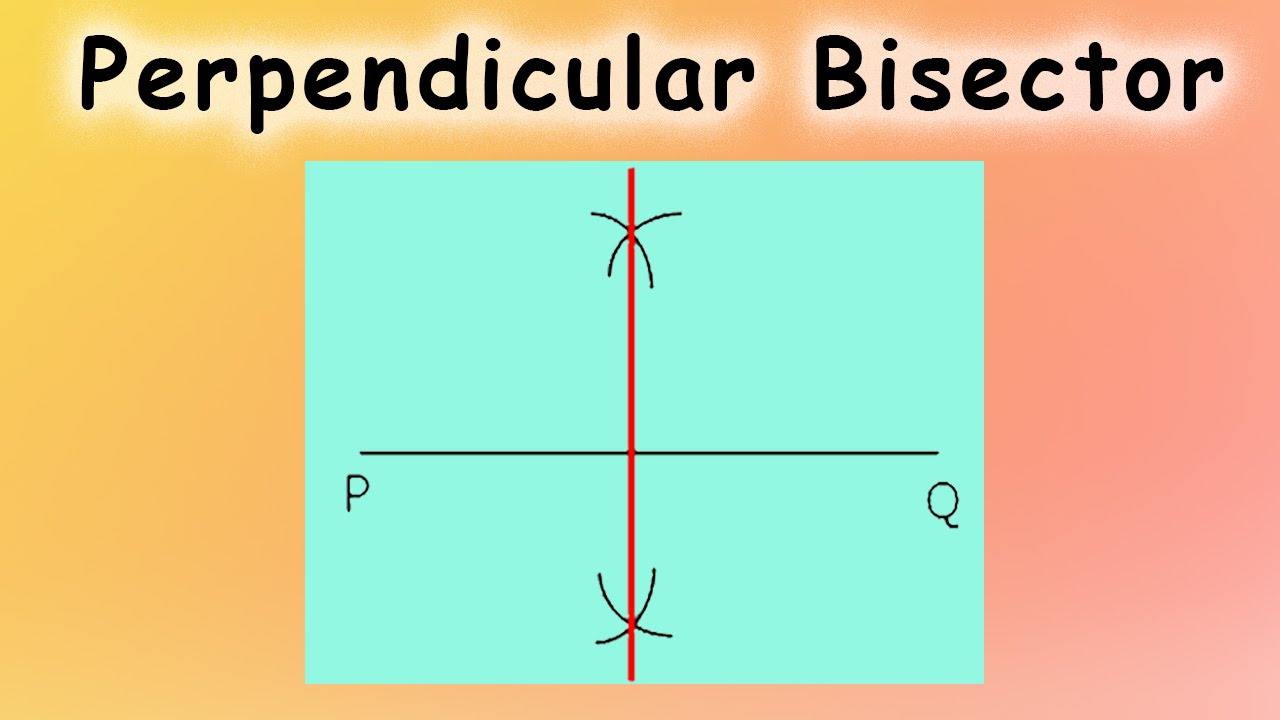
A perpendicular bisector is a line that crosses another line at a 90-degree angle, or it is the split of anything into two equal or congruent halves. It might be a line, ray, or segment that divides another line segment into two equal halves at a 90-degree angle.
What Is A Perpendicular Bisector: Perpendicular Bisector Definition Geometry
According to alphanewscall.com , What is a perpendicular bisector? How can an archaeologist estimate the size of a plate if just a portion of it has been discovered? How does a landscaper evaluate sprinkler placement for the most efficient use of water?
Perpendicular bisector definition: A bisector is anything that divides an item into two equal pieces. Typically, this “something” is a line or a segment. The definition of a perpendicular bisector is that it aids in the determination of the midpoint of a line.
Equation For Perpendicular Bisector
Let’s look at the definition of perpendicular bisector from an equation standpoint. Here is how to solve for the perpendicular bisector equation:
Step 1: Find the mid-point between the two points.
To calculate the midpoint of two points, use the midpoint formula: [(x1 + x2)/2, (y1 + y2)/2]. This implies you’re simply taking the average of the two sets of points’ x and y coordinates, which brings you to the midpoint of the two coordinates. Assume we have the (x1, y1) coordinates of (2, 5) and the (x2, y2) coordinates of (8, 3). Here’s how to determine the intersection of those two points:
[(2+8)/2, (5 +3)/2] (5, 4) = (10/2, 8/2)
The midpoint coordinates of (2, 5) and (8, 3) are (5, 4).
Step 2: Calculate the slope of the two points.
Simply enter the two points into the slope formula to obtain the slope: (y2 – y1) / (x2 – x1). The slope of a line is calculated by dividing the distance of its vertical change by the distance of its horizontal change. Here’s how to calculate the slope of the line that connects the points (2, 5) and (8, 3)
(3-5)/8-2 = -2/6 = -1/3
The line has a slope of -1/3. To find this slope, reduce 2/6 to its simplest terms, 1/3 because both 2 and 6 are equally divisible by 2.
Step 3: Find the inverse of the slope of the two points.
To get the negative reciprocal of a slope, just take the slope’s reciprocal and flip the sign. Simply swapping the x and y coordinates and changing the sign yields the negative reciprocal of a number. 1/2’s reciprocal is -2/1, or simply -2; -4’s reciprocal is 1/4.
Because 3/1 is the reciprocal of 1/3 and the sign has been reversed from negative to positive, the negative reciprocal of -1/3 is 3.
Step 4: Write a line equation in slope-intercept form.
A slope-intercept equation is y = mx + b, where “x” and “y” represent any x and y coordinates in the line, “m” represents the slope of the line, and “b” represents the y-intercept of the line. The y-intercept is the point at which the line meets the y-axis. Once you’ve written this equation down, you may start looking for the equation of the perpendicular bisector of the two points.
Step 5: In the equation, enter the negative reciprocal of the original slope. The negative reciprocal of the slope of the points (2, 5) and (8, 3), respectively, was 3. Plug the 3 into the “m” in the equation y = mx + b.
y = mx + b = y = 3x + b = y = 3x + b
Step 6: You are already aware of the fact that the midpoint of the points (2, 5) and (8, 3) is (5, 4). Because the perpendicular bisector passes through the midpoint of the two lines, the coordinates of the midpoint may be plugged into the equation of the line. Simply enter (5, 4) into the line’s x and y coordinates.
(5), (4) —> y = 3x + b = 3(5) + b = 15 + b
Step 7: Determine the intercept.
You have discovered three of the four variables in the line’s equation. You now have enough data to calculate the remaining variable, “b,” which is the y-intercept of this line. To determine the value of the variable “b,” just isolate it. Simply take 15 off both sides of the calculation.
4 = 15 + b
b = -11
Step 8: Write the perpendicular bisector equation.
To create the equation of the perpendicular bisector, just enter the slope of the line (3) and the y-intercept (-11) into the slope-intercept equation of a line. You should not enter any terms into the x and y coordinates since this equation allows you to locate any coordinate on the line by entering any x or y coordinate.
y = mx + b
y = 3x – 11
The perpendicular bisector of the points (2, 5) and (8, 3) has the equation y = 3x – 11.
Perpendicular Bisector Properties
- A perpendicular bisector splits or bisects a line segment into two parts.
- A perpendicular bisector intersects (or is perpendicular to) a line segment at right angles.
- Each point on the perpendicular bisector is equidistant from both ends of a line segment.
- When dealing with practical geometry, you will frequently encounter the use of perpendicular bisectors, such as when attempting to construct an isosceles triangle or determining the center of a circle.
Perpendicular Bisector Theorem
We apply the perpendicular bisector theorem when we have a perpendicular bisector in the picture.
The converse is also true: if a point is equidistant from the ends of a segment, it sits on the perpendicular bisector.
This theorem teaches us that there is a succession of locations equidistant from the ends of a line segment that, when joined together, may create a line to the middle of that line segment at a right angle.
How To Find Perpendicular Bisector?
It is fairly straightforward to find a perpendicular bisector. You may have guessed how to accomplish this from reading the part above that defines a perpendicular bisector.
An easy method to determine a perpendicular bisector is to measure the line segment you need to bisect. Then, divide the measured length by two to determine the midway. Draw a line at a 90-degree angle out from this midpoint. If you have a ruler, that’s all you need to do to find the perpendicular bisector!
How To Construct A Perpendicular Bisector?
Assume we are given the line segment AB. We want to build a line that intersects this section at a right angle and divides it into two equal halves.
To begin, we draw two circles of length AB. Center A will be in the first, while Center B will be in the second. Draw segments AC and BC and label the junction of these circles as C. The ABC triangle will be equilateral.
The angle ACB must then be bisected. The intersection of the angle bisector and the line AB is denoted by the letter E.
Perpendicular Bisector Proof
We may first demonstrate that E is the centre of AB by demonstrating that AE=BE.
ACE=BCE because CE bisects ACB and CE is equal to itself, and AC=BC since they are both legs of an equilateral triangle. As a result, because the triangles ACE and BCE have the same two sides and the same angle between those sides, the two triangles are congruent. This indicates that the third sides, AE and BE, are the same. As a result, E is the centre of segment AB, and CE bisects it.
The two resultant angles, CEA and CEB, are right angles since they are congruent and contiguous. As a result, CE is also perpendicular to AB.
How To Construct Perpendicular Bisector Of A Triangle?
Here is how you can construct a perpendicular bisector of a triangle:
With a ruler and compass, you can simply draw the perpendicular bisector triangle.
Begin by drawing the perpendicular bisector of a line segment S with endpoints X and Y:
- Draw arcs of the same radius centered at X and Y by opening the compass more than half the distance between X and Y.
- These two arcs intersect at two places. We’ll refer to them as points P and Q.
- Draw the line segment M, which is the perpendicular bisector of the line segment S, where the arcs intersect (i.e. link point P and point Q).
Now, we’ll do the same thing on all three sides of the triangle to draw its three perpendicular bisectors (Ma, Mb, and Mc):
Read Here– The Axis Of Symmetry: What Is It, Equation, How To Find It, And Formula
How Is Constructing A Perpendicular Bisector Similar To Constructing An Angle Bisector?
Angle bisectors divide an angle into two congruent angles, whereas perpendicular bisectors are two lines that intersect at the midway of a line to produce right angles. They vary in that one cuts angles and the other cuts line segments. They are similar in that they both cut things in a triangle.
The perpendicular bisector theorem deals with congruent triangle segments, allowing for congruent diagonals from the vertices to the circumcenter. The angle bisector theorem, on the other hand, deals with congruent angles, resulting in equal lengths from the incenter to the side of the triangle.
Perpendicular Bisector Calculator
A perpendicular bisector calculator requires you to enter 4 values. Suppose you have two lines PQ and AB. You need to enter (x,y) coordinates of PQ and (x,y) coordinates of AB.
After entering the value, you will have to simply press the calculate button. The calculator would give you a perpendicular bisector equation.
Perpendicular Bisector In Real Life – Some Examples
Table legs, for instance, are a perfect example of a perpendicular bisector, are generally perpendicular to the tabletop, while walls are usually perpendicular to the floor. Bisector: This term refers to “anything that splits perfectly in half.” For example, if you snap a KitKat finger and the two pieces that remain are identical in size, you have bisected it.
The following are real-world instances of perpendicular lines. :
- The football field
- Crossing of railway tracks
- First-aid supplies
- Building a house in which the floor and the walls are perpendiculars
- Television
- Window decorations